It was in 1896 that Becquerel in France detected, by chance, faint traces of the existence of the nucleus in the atom. For many years after that the study of nuclear physics remained a curiosity and intellectual challenge to scientists, but had little practical use outside its own field. The situation changed totally in the 1930s with discoveries that culminated in the cataclysmic demonstrations near the end of the second world war of the immense energy locked up by the force that holds the atomic nucleus together. An unprecedented and irrevocable step had been taken in the degree of power available to humankind with dramatic consequences for good and ill.
Today, nuclear physics has entered into our modern world in a significant way. It influences other branches of science: chemistry, biology, archaeology, geology, engineering, astrophysics and cosmology. It is used widely in society at large – in industry, the environment, medicine, defence, criminology, power production and many other areas. Applications are found even in religion and the arts, where equipment and methods developed originally for nuclear research have found novel application. However, the exploitation of such a powerful force carries with it some danger and is the subject of much debate.
The main aim of this book is to address the broad range and variety of the techniques and applications of nuclear physics used today. The basic physics underlying them is given first in order that the benefits and drawbacks can be properly appreciated. No particular stance is taken on controversial issues. The view taken is that a proper understanding of the subject is important and necessary in order that wise decisions can be taken about how nuclear energy and nuclear radiation should be used.
Essential nuclear physics for understanding the applications is given in this first chapter. Other chapters in Part I give further development of the topics introduced in Chapter 1. The coverage of the applications in Part II is by no means exhaustive. It is intended broadly to inform the reader and provide a suitable preparation for those students who plan to take more advanced courses on any of the separate topics.
Unlike atomic physics, which is underpinned by electromagnetism, there is no fundamental theoretical formalism that completely describes nuclei and nuclear behaviour. For example, there is no formula, analogous to Coulomb’s law for the force between two electric charges, which exactly expresses the force between two basic constituents of the nucleus. Progress in understanding the nature of nuclei is made using approximate models, each of which provides insight into the complexity of the real situation, but with a limited range of applicability. Models are drawn from analogy with classical and other branches of physics and are formulated to be consistent with observed properties and behaviour. Conceptual models played a vital role in the first few decades of the twentieth century when the basic framework of the subject was being established. The following section is a short account of this early period.
The history of the nucleus dates from the latter years of the nineteenth century with the observation by Becquerel in 1896 of the fogging of photographic plates by an unknown radiation emanating from uranium-bearing rocks. He had encountered radioactivity. Detailed studies of this new phenomenon began to be made, notably by Marie and Pierre Curie in France and by Ernest Rutherford, who had come to England from New Zealand earlier in 1895 to work in Cambridge with J. J. Thompson (who discovered the electron in 1897). It was soon revealed that there are three, distinctly different types of radiation emitted by radioactive substances. They were called alpha (α), beta (β) and gamma (γ) rays – terms which have been retained to this day.
The most far-reaching advances in the subject during this early phase were made by Rutherford. He and his co-workers, first in Canada (1898–1907) and later in Manchester, England (1907–1919), began an intensive study of the new radiations. All the laws governing radioactive decay were established. It was shown that α- and β-radioactive decays change the nature of the element and that a particles are helium nuclei. Beta particles were found to be the same as electrons, and γ rays were identified as energetic photons (electromagnetic radiation).
Rutherford used α particles to probe the structure of the atom itself. It was already known that the atom consisted of positively charged and negatively charged components, but there were two very different models for describing how these components might combine to form an atom. The ‘planetary9 model assumed that light, negatively charged electrons orbit a heavy, positively charged nucleus. The problem with this model was that the electrons would be constantly accelerating and should radiate energy as electromagnetic waves, causing the atom to collapse. In an alternative model, proposed by J. J. Thompson, the electrons are embedded and free to move in an extended region of positive charge filling the entire volume of the atom. Such an atom would not collapse, but Thompson had difficulty in developing his model. For example, he was never able to account successfully for the discrete wavelengths observed in the spectra of light emitted by excited atoms.
The crucial breakthrough came from experiments carried out by Rutherford and his team in Manchester, who were studying the passage of a particles through matter. It was noted that very thin foils of gold caused a particles to be deflected occasionally through large angles and even in the backward direction. Rutherford realized that this could not be due to the combined effect of a large number of small-angle deflections and could only be explained if the a particle had encountered a tiny, but heavy, charged entity less than 1/1000th of the atom in size. Undaunted by the fact that the planetary model should not exist according to classical theory, he proposed that the atom does consist of a small, heavy positively charged centre surrounded by orbiting electrons which occupy the vast bulk of the atom‘s volume. The simplest atom, hydrogen, consisted of a proton and a single orbital electron.
Many atomic masses were known to be approximately integer multiples of a basic unit of mass about 1% lighter than the mass of the hydrogen atom. For example, the atomic masses of carbon, nitrogen and oxygen, expressed in these units, are approximately 12.0, 14.0 and 16.0, respectively. However, there are notable exceptions, such as the element chlorine, which has an atomic mass of 35.5 of these units. The idea that an element could consist of differing isotopes, which are atoms whose nuclei have different masses but the same charge, was put forward by Soddy in 1911. This explained the existence of anomalous atomic weights, like chlorine, but reinforced an idea, which was current at that time, of nuclei consisting of different numbers of protons and electrons bound together in some way. The proton-electron model persisted for many years until developments in quantum mechanics exposed its shortcomings. No one, for example, could explain why an electron with enough energy to be emitted in β decay was not emitted instantly. Indeed, an estimate of the energy required to keep an electron inside the nucleus (see Problem 1.3) was many times greater than the energies seen in β decay, and an attractive force strong enough to do this would have effects on atomic spectra, which were not observed.
Little progress was made until 1932, when James Chadwick proposed the existence of the neutron, an uncharged nuclear constituent whose existence had been anticipated by Rutherford as early as 1920. 1 Bothe and Becker, in 1930, had observed highly penetrating, uncharged radiation from the a-particle bombardment of beryllium. In 1931, F. Joliot and I. Curie measured fast protons emerging from paraffin exposed to this radiation. They surmised that the protons were recoiling from being bombarded by electromagnetic radiation and deduced that, if this were the case, the photon energy would have to be 50MeV – more energetic than the estimated total energy released in the reaction. Chadwick compared the recoils of protons and nitrogen from different bombarded materials and correctly deduced the mass of the neutral radiation particle to be approximately equal to that of the proton. The neutron was the critical missing ingredient for understanding nuclei. Heisenberg, Majorana and Wigner then took steps to establish the framework that forms the basis of the modern picture of the nucleus consisting of nucleons (neutrons and protons) held together by a short-range force whose strength is independent of the type of nucleon.
From the results of subsequent experiments, in which particles were collided at very high energies, it has become apparent that neutrons and protons themselves have an underlying structure composed of three sub-nucleonic particles, which have been called quarks. Particle physics deals with the world of the quark and all other particles still thought to be fundamental. These aspects are not dealt with in this text. The structure of neutrons and protons is discerned only at very high energies and, for all practical purposes concerning nuclear structure research and nuclear physics applications in the modern world, the neutron-proton model of the nucleus is entirely adequate.
An atomic nucleus is the small, heavy, central part of an atom consisting of A nucleons: Z protons and N neutrons; A is referred to as the mass number and Z, the atomic number. Nuclear size is measured in fermis (also called femtometres) where 1fm = 10 −15 m.
The basic properties of the atomic constituents can be summarized as follows:
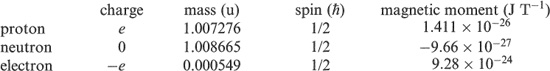
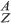
Charge: Protons have a positive charge of magnitude e = 1.6022 × 10 −19 C (coulombs) equal and opposite to that of the electron. Neutrons are uncharged. Thus, a neutral atom (A, Z) contains Z electrons and can be written symbolically as XN.
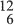
Mass: Nuclear and atomic masses are expressed in atomic mass units (u), based on the definition that the mass of a neutral atom of C6 is exactly 12.000 u (1 u = 1.6605 × 10 −27 kg – see Appendix A).
Spin: Each of the atomic constituents has a spin 1/2 in units of ħ (= h/2π) and is an example of the class of particles of half-integer spin known as fermions. Fermions obey the exclusion principle, first enunciated by Wolfgang Paull in 11925 which determines the way electrons can occupy atomic energy states. The same rule applies to nucleons in nuclei, as we discuss in the next section.
Magnetic moment: Associated with the spin is a magnetic dipole moment. Compared with the magnetic moment of an electron, nuclear moments are very small. However, they play an important role in the theory of nuclear structure. It may be surprising that the uncharged neutron has a magnetic moment. This reflects the fact that it has an underlying quark sub-structure, consisting of charged components. An important application of nuclear moments, based on their behaviour in electromagnetic fields, is the technique of magnetic resonance imaging or nuclear magnetic resonance, which is described in Chapter 9.
Isotopes of an element are atoms whose nuclei have the same Z but different N. They have similar electron structure and, therefore, similar chemical properties. For example, hydrogen has three isotopes: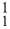 
H0,
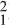H1 and 
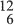H2, whose nuclei are, respectively, the proton p, the deuteron d, and the triton t. Carbon has three, naturally occurring isotopes: C6,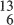 
C7 and 
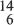C8. Nuclei with the same N and different Z are called isotones, and nuclides with the same mass number A are known as isobars. In a symbolic representation of a nuclear species or nuclide, it is usual to omit the N and Z subscripts and include only the mass number as a superscript, since A = N + Z and the symbol representing the chemical element uniquely specifies Z.
Inside a nucleus, neutrons and protons interact with each other and are bound within the nuclear volume under the competing influences of attractive nuclear and repulsive electromagnetic forces. This binding energy has a direct effect on the mass of an atom.
In 1905, Einstein presented the equivalence relationship between mass and energy: E = mc 2 . The speed of light c is very large and so even a small mass is equivalent to a large amount of energy* The complete conversion of 1 g of matter releases about as much energy as 20000 tons of TNT. On the atomic scale, 1 u is equivalent to 931.5 MeV/c 2 , which is why energy changes in atoms of a few electron volts cause insignificant changes in the mass of the atom. Nuclear energies, on the other hand, are millions of electron volts and their effects on atomic masses are easily detectable. For example, the mass of an atom can be measured to high precision (of the order 1 part in 10 6 ) in a modern mass spectrometer, and the error in the mass-energy of 12 C, measured to 1 part per million, is about 11 keV. Mass differences can be determined to even greater precision with these instruments, and many relative masses are known to an accuracy of a few keV.
Relative masses of nuclei can also be determined from the results of nuclear reactions or nuclear decay. For example, if a nucleus is radioactive and emits an α particle, we know from energy conservation that its mass must be greater than that of the decay products by the amount of energy released in the decay. Therefore, if we measure the latter, we can determine either of the initial or final nuclear masses if one of them is unknown. An example of this is presented in Section 1.5.1.
The binding energy of a nucleus B is the energy required to separate it into its constituent neutrons and protons. The mass of an atom, therefore, is less than the mass of its constituents by the mass equivalent of B. Symbolically, this is written as
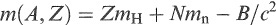
(1.1)
where m(A, Z), mH and mn are the atomic masses of the nuclide (mass number A and atomic number Z), a hydrogen atom and a neutron, respectively, and B is expressed in energy units. This equation assumes that differences in the average binding energies of electrons in different atoms are negligible. All the effects of forces acting on the nucleons inside a nucleus are contained in the binding-energy term. Variations in atomic masses due to variations in binding energy are invariably small compared with an atomic mass unit, which is equivalent to nearly 1 GeV. For this reason, an atomic mass is often presented in the literature as the difference m(A,Z) – A between the mass (in atomic mass units) and the atomic number. This is called the mass excess (me). Mass excesses of a number of nuclides are listed in Appendix F in units of micro atomic mass units (μu). 2
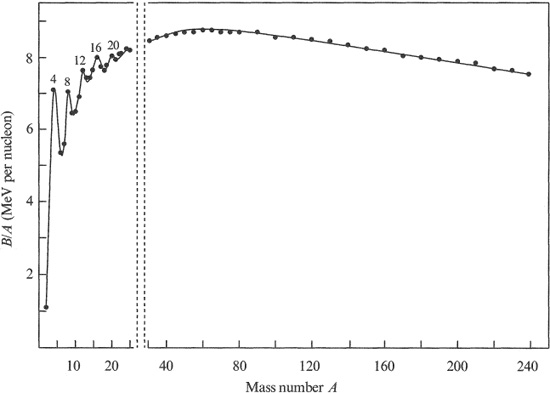
Nuclear binding energy increases with the total number of nucleons A and, therefore, it is common to quote the average binding energy per nucleon (B/A). The variation of B/A with A is shown in Figure 1.1 and reveals a number of important features. There is an initial sharp rise with A to a broad maximum of about 8.6 MeV per nucleon near a mass number of 60. This is followed by a gradual decrease to about 7.6 MeV per nucleon for the heaviest nuclei. Nuclei with A greater than 238 are not found in significant quantities in the earth‘s crust. Several sharp peaks in the light-nuclear region correspond to the nuclei 4 He, 8 Be, 12 C, 16 O, 20 Ne and 24 Mg. The 4 He nucleus (α particle) has a particularly stable structure, and the A and Z of the other nuclei are multiples of the α particle. Their extra stability is taken as evidence that they have a structure which bears some resemblance to that of a collection of a particles.
The overall form of the curve in Figure 1.1 is the result of the combined effect of the nuclear and electrostatic (Coulomb) forces and is discussed in some detail in the next chapter. The nuclear force is very complex and it is not possible to deduce its form precisely. However, the important property we need for the present discussion is that it operates over a very short distance of a few fermis. In a light nucleus, where there are only a few nucleons, any one of them interacts with all the other nucleons and, therefore, its binding energy increases with mass number. However, the size of a nucleus increases with A and when it exceeds that of the range of the internucleon force, the nucleon will interact only with its neighbours which lie within that range. Consequently, the binding energy of a nucleon due to the nuclear force alone will tend to approach a constant value at large A. The Coulomb force, on the other hand, acts over a much larger range, and the electrical potential energy per proton grows steadily as Z increases. It is of opposite sign to the nuclear binding energy and, eventually, this negative term becomes the determining factor causing the fall in B/A beyond A ~ 60.
Figure 1.1 Binding energy per nucleon of stable nuclei plotted as a function of mass number i. The horizontal scale below A = 30 is twice that above A = 30.
From the form of the binding energy curve, it is clear that when A 120, energy could be released by breaking the nucleus into two, roughly equal fragments. This is called fission and it occurs spontaneously if A is sufficiently large or if a very heavy nucleus, like 235 U or 238 U, is excited to a higher energy state. At the other end of the mass scale, energy can be gained by combining two light nuclei together in a fusion reaction to form a heavier system with higher B/A. The fission process is already being exploited for commercial power production, and nuclear fusion is a potential source of energy for the future. Some of the underlying physics of fission and fusion is covered in Sections 2.2, 4.5 and 4.6. A fuller discussion of their practical importance is presented in Chapters 10 and 11.
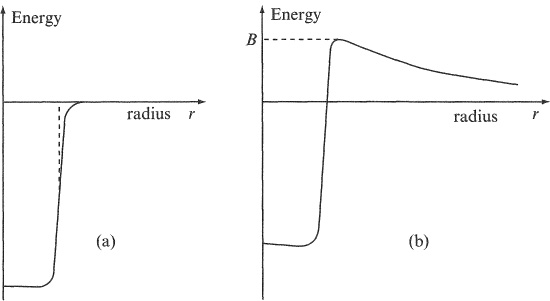
It can be shown to a first approximation that a nucleon in a nucleus experiences an average (or mean) attractive energy due to the strong nuclear interaction with its neighbours. This is approximately constant in the nuclear interior and, for the uncharged neutron, it can be represented, as in Figure 1.2(a), by a potential well. This well does not have a sharp edge because of the range of the nuclear force and because the distribution of nucleons in the surface of a nucleus is diffuse. Outside the nucleus, the neutron experiences no force and its potential energy (PE) does not change until it approaches the nuclear surface. There, under the influence of the attractive force, it ‘fails‘ into the nuclear interior with a gain in kinetic energy corresponding to the decrease in PE.
A proton experiences in addition a repulsive Coulomb PE, Vc, due to its positive charge. The general effect of this is shown in Figure 1.2(b). Outside the nucleus, where there is no nuclear force acting on the proton, the form of Vc is that due to a point charge. Inside the nucleus, the Coulomb energy reduces the depth of the total potential for protons compared with that for neutrons by an amount that increases with the nuclear charge Ze. However, compared with the nuclear potential, the difference is always small and can often be neglected to a first approximation. Near the edge of the nucleus, the total PE reaches a maximum B of what is called the Coulomb barrier. This energy barrier maintains the stability of the Universe, since it is what prevents low-eriergy (charged) nuclei coming into contact with each other and initiating nuclear reactions.
Figure 1.2 Schematic representation of the potential energy (PE) experienced by (a) a neutron and (b) a proton, as a function of distance r from the centre of a nucleus. Outside the nucleus, the proton experiences the electric force only and its PE is given by the Coulomb potential: Vc = Ze 2 /4πε0r
A model of a nucleus is to consider that neutrons and protons exist inside nuclei in certain, allowed energy states or levels within the average potential well Heisenberg’s Uncertainty Principle ∆x∆p ≥ ħ helps us to understand why nuclear energies must be large. The small nuclear size ∆x implies a large uncertainty in the momentum of a nucleon confined within it. Hence, there is a large uncertainty in its kinetic energy which, typically, is several MeV. We can make the argument more quantitative and, at the same time, illustrate the existence of discrete energy states, by choosing a particular form for the confining potential well
The simplest example is that of a particle in a one-dimensional box, which we will take to be of size a centred at x = 0. Solving the Schrodinger equation for this problem, together with the boundary condition that the wave function must vanish at the boundary of the box, one finds that solutions are only possible for certain values of the energy, known as eigenvalues (see Appendix B):
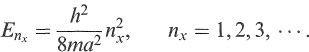
(1.2)
These are the discrete levels of the particle in the box. The corresponding solutions are
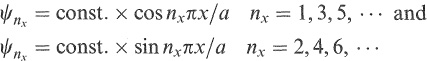
(1.3)
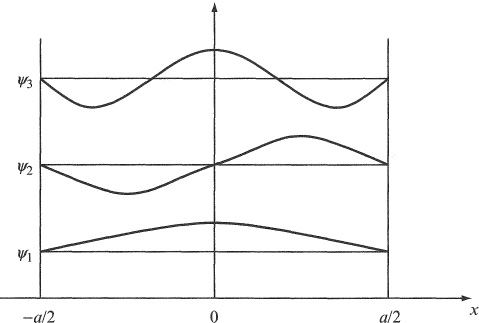
the first few of which are shown in Figure 1.3. Note that they vanish at x = ± a/2 as required.
A very simple model of a nucleon in a nucleus is that of a particle confined inside a cubic box of side a. The above results in one dimension are easily generalized to this case (see Appendix B) and we quote the main result. The energy eigenvalues are now given by
Figure 1.3 Wave functions representing the lowest three states of a particle confined to a one-dimensional box of side a.
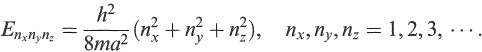
(1.4)
The energy of the lowest state a nucleon can occupy is given, with nx = ny = nz = 1, as E111 = 3h 2 /8ma 2 . Substituting for h 2 (e.g. from Appendix A), with m = 1 u, and taking a= 10fm for a typical nuclear size, we obtain E111 ~ 6 MeV. Other allowed states are given by different combinations of nx, ny and nz (see Problem 1.5).
In general, a particle in a three-dimensional potential may move with orbital angular momentum with respect to the centre of the well. Angular momentum, like energy, is a conserved quantity and states are labelled according to angular momentum as well as energy.
In quantum mechanics, angular momentum occurs in discrete amounts. Orbital angular momentum is specified by a positive, integer quantum number ℓ (≥ 0) and an integer projection quantum number m along an axis, which is normally taken to be the z-axis. The magnitude of the total angular momentum L and its z projection Lz are given by
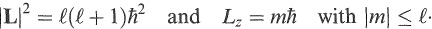
(1.5)
A state with angular momentum number ℓ has (2ℓ + 1) independent projections (sub-states) all with different m values between −ℓ and +ℓ Individual nucllons si nuclei occupy states which can have angular momentum ℓ = 0, 1, 2, 3 …. Thess ere referred to as s, p, d, f … states, as are the corresponding electron states in atoms.
Angular momentum is also associated with the intrinsic spin property of particles referred to in the previous section. The quantum numbers (s and ms) for spin angular momentum S may be either integral or half integral, with equations for S and its projection Sz similar to Equation (1.5). As stated earlier, a proton, neutron or an electron each has spin quantum number s=l/2 and there are two projections: ms = ±1/2 given by the (2s+1) rule.
Neutrons and protons in a nucleus occupy energy states subject to the exclusion principle rule that no two identical particles can have the same set of quantum numbers. Thus, two protons and two neutrons can exist in the lowest state provided that their spins are anti-parallel to each other, i.e. one has spin ‘up’ and the other spin ‘down’. This forms the 4 He nucleus or α particle, which has a total spin of zero. As we have noted, the α particle is particularly stable, requiring over 20 MeV to remove either a neutron or proton. In nuclei heavier than 4 He, the additional nucleons must occupy states at progressively higher energies as more nucleons are added.
Like atoms, nuclei can exist in different energy levels corresponding to different arrangements of the nucleons in their allowed states. At low excitation, these levels occur at discrete energies, and each nuclide has its own characteristic energy spectrum. That for 12 C is shown in Figure 1.4 up to an excitation energy of 10 MeV. The integer labelling each level is a quantum number I specifying its total angular momentum in units of ħ. The total angular momentum of a state I is a combinatton of L, the total orbital angular momenta of all the A nucleons in the nucleus, and S, the vector sum of their intrinsic spins. In nuclear physics, the term ‘spin’ is used to denote this total angular momentum I and, hereafter, this is what the term spin by itself will mean when talking about nuclei. As we shall see in Chapter 2, most of the nucleons in a nucleus combine in pairs, each contributing a net angular momentum or spin of zero, which is why the ground states of all nuclei with even N and even Z have a total spin of zero.
A nucleus in an excited state normally remains there for a very short time. Often, it decays or becomes de-excited by emitting electromagnetic radiation in the form of a γ ray while undergoing a transition to a state lower in energy. However, if the energy of the state is high enough, the nucleus may decay by emitting a particle such as a neutron or α particle. For example, the energy of the second excited state in 12 C at 7.654 MeV is above that required for the nucleus to separate into an α particle and 8 Be. As we shall see in Chapter 11, this state plays a key role in stellar evolution and the creation of elements inside stars.
Figure 1.4 Energy-level spectrum of 12 C; each level is labelled by its energy in MeV and total angular momentum (or spin) quantum number. Also shown on the same energy scale is the state corresponding to separating 12 C into an α particle and a 8 Be nucleus.
The energy of a quantum state that decays is not precisely defined. This is a consequence of the uncertainty principle and it manifests as a spread in energy (or energy width Γ), which increases as the lifetime of the state decreases. As the excitation energy of a nucleus increases, the average width Γ increases. Also, the extra energy means that the levels become more closely spaced because there are many more ways the energy can be shared among the nucleons and each way corresponds to a different energy level. The levels begin to overlap in energy and, eventually, the energy spectrum becomes a continuum in which an individual level cannot be discerned.
The occurrence of nuclei and their relative abundance in nature reveal important aspects of nuclear structure which are considered further in Chapter 2. Known stable and unstable (radioactive) nuclides are presented, according to their Z and N numbers, in Figure 1.5. In this diagram, the stable nuclei and very long-lived unstable nuclei (black squares) follow a particular line referred to as the line or valley of stability.
Figure 1.5 Stable and unstable nuclei plotted according to proton number Z and neutron number N. Regions of known proton-rich and neutron-rich unstable nuclei are indicated on either side of the band of stable nuclei (and very long-lived unstable nuclei), which are represented as black squares.
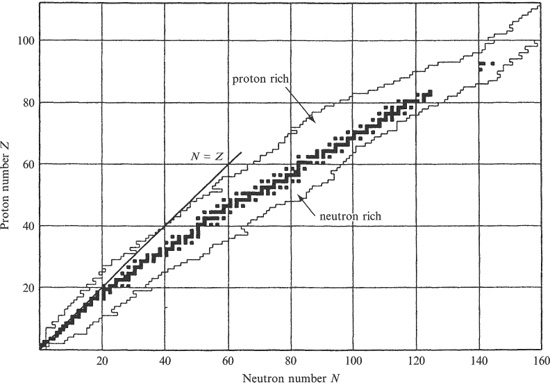
A nucleus lying either above or below this line has a binding energy greater than the minimum value corresponding to its particular mass number A and, therefore, is unstable. Some of the excess energy of such an unstable nucleus may be recovered by converting a neutron into a proton or vice versa. There is a force in nature which allows this to occur, called the weak nuclear force. Its strength is about 10 −12 times that of the strong force and it operates over an even shorter range. Consequently, it plays no part in holding the nucleus together. As we shall see in the next section, its importance lies in the fact that it can cause a neutron-rich or proton-rich nucleus to change into a more stable form in a process called β radioactivity.
There is an upper mass limit to the line of stability at 209 Bi. As A increases beyond this point, it becomes increasingly likely that a nucleus will lose mass by emitting an α particle and be transformed into a more stable product. Naturally occurring thorium and uranium nuclei decay in this way, albeit with very long average lifetimes. Alpha and beta radioactivity and the laws governing these processes are discussed in the next section and also in Chapter 3.
In radioactive decay, an unstable nuclide or ‘parent’ is transformed into a more stable nuclide called the ‘daughter’. If the daughter product is also radioactive, the process continues in a decay chain until a stable product is reached. Radioactivity is a random process. We cannot know exactly when a given unstable nucleus will decay and can only specify a probability per unit time that it will do so. This is normally described by the half-life (t1/2), which is the time taken for half the nuclei in a sample to decay.
All naturally occurring, and the majority of artificially produced, radioactive nuclei are either α active, β active or (occasionally) both and emit a combination of α, β and γ radiation. Those that continue to exist in the environment, together with cosmic rays from outer space, generate the background radiation to which we all are subjected. Artificially produced unstable nuclei may decay by emitting protons, neutrons or even heavy ions. In spontaneous fission, very heavy fragments are emitted. Some of these decay modes are dealt with at the appropriate places later in the text. This section deals with α, β and γ radioactivity only, describing the changes that occur and the radioactivity decay laws. Further details and insight into the underlying physics are covered in Chapter 3.
Many naturally occurring, heavy nuclei, with 82 < Z ≤ 92, and artificially produced transuranic elements (Z > 92) decay by α emission, in which the parent nucleus loses both mass and charge: (A,Z) → (A − 4, Z − 2). The eaughter may yo may yno tb stable, but it invariably lies closer to the region of stable nuclei which, eventually, is reached. The a particle is emitted in preference to other light particles (d, t, 3 He…) because energy must be released in order for the decay to take place at all. The α particle has a very stable, tightly bound structure and can be emitted spontaneously with positive energy in α decay, whereas d, t or 3 He decay would require an input of energy (see Problem 1.6).
The energy released in a decay (Qα) is given by the difference in mass energy between the parent nucleus and final products and appears as kinetic energy shared between the outgoing particles. Thus, we can write
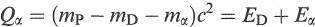
(1.6)
where mP, mD and mα are the masses of the parent, daughter and α particle, respectively, and ED and Eα are the kinetic energies of the daughter and α particle.
Assuming the decaying nucleus is at rest, the daughter must recoil in the opposite direction to the α. particle and with the same momentum, i.e. mDυD = mαυα. The ratio of their kinetic energies, therefore, is
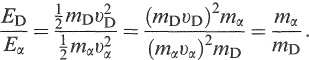
(1.7)
From Equations (1.6) and (1.7), we can determine Ea and ED uniquely in terms of Qa, mo and ma, since
(1.8)
Alternatively, if we have measured Eα, we can use the equations to determine mp or mD if either of them is unknown.
For example, 238 U emits an α particle of kinetic energy 4.196 MeV. The daughter is 234 Th and its mass is obtained from Equations (1.6) and (1.8) as
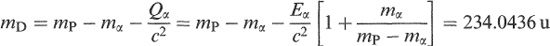
where we have substituted Eα/c 2 = 4.196 (MeV)/931.5 (MeVu −1 ) = 0.0045 u, and 238.0508 u and 4.0026 u for the masses of 238 U and the α particle, respectively. Note that it is accurate enough to use mP – mα for mD (neglecting Qα/c 2 ) in the factor multiplying Eα/c 2 ,
Unstable nuclei, which are described as either neutron rich or proton rich (see Figure 1.5), decay towards the line of stability into other isobaric nuclei by positive or negative β-particle emission or by the capture of an atomic electron.
A negative β particle is identical to an electron (e − ) and when it is emitted, the charge on the nucleus increases by one unit. Conversely, when a positive β particle is emitted, the nuclear charge decreases by one unit. A positive β particle is called a positron (e + ). It behaves like a positively charged electron and has the same mass. It is an example of antimatter, the existence of which was predicted by Dirac several years before it was first identified by Anderson in 1932.
Unlike α particles, β particles are emitted with a continuous spectrum of energies. An example is shown in Figure 1.6. The maximum energy (end point) in the spectrum is the energy expected according to the mass–energy relationship, but the average electron energy is only about a third of this. Energy, apparently, is missing. Wolfgang Pauli, in 1931, accounted for this apparent violation of energy conservation by postulating the existence of a third, undetected particle in the decay, which Enrico Fermi later called a neutrino (υ) (‘little neutral one’). The neutrino is an uncharged fermion (spin 1/2), with zero or negligible rest mass, which interacts extremely weakly with matter. It is difficult to detect the neutrino and it was not until the 1950s, some 25 years after it was postulated, that Reines and Cowan, in a very sophisticated experiment incorporating a nuclear reactor, gave objective proof of its existence.
Beta decay is considered to be the transformation of one of the nucleons in the nucleus from a neutron into a proton or vice versa, creating light particles, called leptons, in the process and leading to a more stable final product. The two processes may be written symbolically as
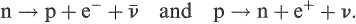
(1.9)
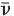
The leptons (e−, υ) and anti-leptons (e + , ) are created by the action of the weak nuclear force, which is why β decay, generally, is a relatively slow process compared with transitions involving the strong force or the electromagnetic interaction. Energy must be conserved and so the transformations given in Equation (1.9) can occur only if the daughter nucleus is lighter (i.e. more stable) than the parent.
Figure 1.6 Energy spectrum of β particles emitted by 210 Bi. From Evans (1955) p. 538.
An alternative to β + decay, for a proton-rich nucleus, is electron capture (EC) in which a proton and an atomic electron are transformed into a neutron and a neutrino:
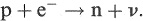
(1.10)
The electron is usually captured from the innermost orbit, or K shell, of the atom, which is why the process is often referred to as K capture. In principle, electrons from less tightly bound atomic shells (L, M, N, etc.) could participate in EC. However, the probability depends on the overlap of the electron wave function with the nuclear volume and this is smaller for L or higher-shell electrons than it is for a K-shell electron.
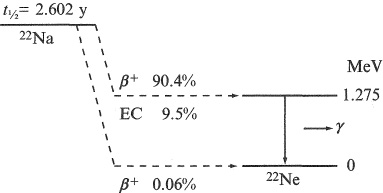
An example of a β-decay energy-level diagram is shown in Figure 1.7 for 22 Na (tl/2 = 2.602 years). In this case, the main β + and EC decay branch is to an excited state of the daughter, which subsequently decays by emitting a 1.275-MeV γ ray. It is common in β decay to have a strong decay branch to an excited state of the daughter. By accurately measuring the γ-energy, as described in Chapter 6, it is possible to identify γ-emitting radioactive isotopes uniquely making them much more useful than pure β emitters for applications such as tracing, irradiation, medical imaging and diagnosis (see Chapters 8 and 9).
As noted earlier, an excited nucleus may lose energy in a transition to a state lower in energy in the same nucleus. When this occurs, most of the transition energy ∆E, which is the energy difference between the initial and final states, may appear in the form of a γ-ray photon.3 Alternatively, the nucleus may de-excite by ejecting an electron from one of the atomic orbits in a competing process called internal conversion. Both these decay modes are due to the action of the electromagnetic force. If the transition energy is sufficiently high, a third type of electromagnetic decay is possible, called internal pair formation, in which an electron–positron pair is created. This process is usually weak, except for very high transition energies, and can only occur if the available energy exceeds that needed to create the pair, which is 1.022MeV.
Figure 1.7 Decay scheme for the positron-emitting radioactive nucleus 22 Na. The intensities of the β + and electron-capture (EC) branches are indicated as percentages.
Gamma-decay and internal-conversion lifetimes are usually very short compared with α- or β-decay lifetimes and are, typically, less than 10 −9 s. However, there are excited states that last for a much longer time. States with readily measurable half-lives are called metastable or isomeric states (isomers) and the transitions are known as isomeric transitions. The term isomer is sometimes applied to a state with a half-life as short as 10 −9 s but, more usually, the lifetime is much longer. We shall see an example of a long-lived isomer at the end of Section 1.5.5.
The probability per unit time that a given nucleus will decay is called the decay constant λ, and if there are N radioactive nuclei in a sample, the rate of decay is given by
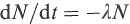
(1.11)
where the minus sign indicates that N is decreasing with time. If the nucleus decays to several different final states (i.e. has several decay branches), the decay constant λ is the sum of the decay probabilities of all the branches.
The solution to Equation (1.11) is
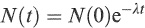
(1.12)
where N(0) is the number of nuclei at t = 0.
The mean life τ is defined as the average lifetime of a radioactive nucleus. From Equation (1.11), the number of nuclei which decay between t and t + dt is just dN = λNdt = λN(0)e −λt dt. Therefore,
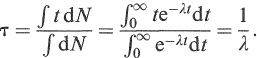
(1.13)
The half-life, t1/2, may be expressed in terms of either λ or τ by substituting N(t1/2) = N(0)/2 in Equation (1.12) and solving for t1/2:
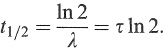
(1.14)
The activity is the rate of decay of a radioactive sample. It is equal to λN (= Nln2/t1/2) and, therefore, follows the same time dependence as N(tμ 10 μ
